4856. Кратчайший путь
Дан неориентированный взвешенный
граф. Найти кратчайший путь между двумя данными вершинами.
Вход. Первая строка содержит натуральные числа n и m
(n ≤ 2000, m ≤ 50000) – количество вершин и рёбер графа. Вторая строка
содержит натуральные числа s и f (1 ≤ s, f ≤ n, s
≠ f) – номера вершин, длину
пути между которыми требуется найти. Следующие m строк содержат по три числа bi, ei и wi
– номера концов i-ого ребра и его вес
соответственно (1 ≤ bi,
ei ≤ n, 0 ≤ wi ≤ 100000).
Выход. Первая строка
должна содержать одно число – длину минимального пути между вершинами s и f.
Во второй строке через пробел выведите вершины на кратчайшем пути из s в f
в порядке обхода. Если путь из s в f не существует, выведите -1.
|
Пример
входа |
Пример
выхода |
|
4 4 1 3 1 2 1 2 3 2 3 4 5 4 1 4 |
3 1 2 3 |
РЕШЕНИЕ
графы –
алгоритм Дейкстры
Анализ алгоритма
Для решения
задачи необходимо реализовать алгоритм Дейкстры. Учитывая ограничения на количество
вершин и рёбер графа, последний следует представлять списком смежности.
Пример
Граф, заданный в
примере, имеет вид:
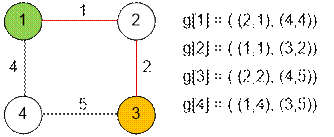
Реализация алгоритма
Граф храним в
списке смежности g, где g[i] содержит
вектор пар (вершина j, длина ребра
между i и j). Объявим дополнительные глобальные массивы для работы алгоритма
Дейкстры:
·
dist[i] хранит
кратчайшее расстояние до вершины i;
·
parent[i] хранит
номер вершины, из которой попали в i двигаясь
из истока по кратчайшему пути.
#define MAX 5010
#define INF 0x3F3F3F3F
int used[MAX], dist[MAX], parent[MAX];
vector<vector<pair<int, int> >
> g;
Функция Relax релаксирует ребро (v, to)
с весом cost.
void Relax(int
v, int to, int
cost)
{
if (dist[to]
> dist[v] + cost)
{
dist[to] = dist[v] + cost;
parent[to] = v;
}
}
Функция Find_Min ищет вершины с наименьшим расстоянием
dist[i] от истока среди тех, до
которых кратчайшее расстояние еще не вычислено (для которых used[i] = 0).
int Find_Min(void)
{
int i, v, min
= INF;
for(i = 1; i
<= n; i++)
if
(!used[i] && (dist[i] < min)) min = dist[i], v = i;
if (min ==
INF) return -1;
return v;
}
Функция path выводит кратчайший путь от истока до вершины v. Для этого используем массив предков.
void path(int
v)
{
if (v == -1) return;
path(parent[v]);
if (parent[v]
!= -1) printf(" ");
printf("%d",v);
}
Основная часть программы. Читаем входные данные. Строим
список смежности g графа.
scanf("%d %d",&n,&m);
sanf("%d %d",&s,&f);
g.resize(n+1);
for(i = 0; i < m; i++)
{
scanf("%d %d
%d",&b,&e,&w);
g[b].push_back(make_pair(e,w));
g[e].push_back(make_pair(b,w));
}
Инициализация глобальных массивов.
Расстояние от истока до истока (dist[s])
полагаем равным 0.
memset(dist,0x3F,sizeof(dist));
dist[s] = 0;
memset(parent,-1,sizeof(parent));
memset(used,0,sizeof(used));
Запускаем цикл алгоритма Дейкстры.
Поскольку граф содержит n вершин, то
достаточно совершить n – 1 итерацию.
for(i = 1; i < n; i++)
{
v = Find_Min();
Если никакую вершину нельзя включить
во множество вершин, до которых кратчайшее расстояние уже посчитано, то
завершаем алгоритм.
if (v == -1) break;
Релаксируем все ребра, исходящие из
вершины v.
for(j = 0; j
< g[v].size(); j++)
{
to = g[v][j].first;
cost = g[v][j].second;
if
(!used[to]) Relax(v,to,cost);
}
Отмечаем, что кратчайшее расстояние
до v уже посчитано (оно находится в
dist[v]).
used[v] = 1;
}
Выводим ответ в зависимости от
значения dist[f]. Если оно равно
бесконечности, то пути до требуемой вершины не существует. Иначе выводим
искомые кратчайшее расстояние и кратчайший путь.
if (dist[f] == INF)
printf("-1\n");
else
{
printf("%d\n",dist[f]);
path(f); printf("\n");
}
Реализация
алгоритма – очередь
с приоритетами, список смежности
Реализуем алгоритм Дейкстры при помощи очереди с приоритетами на списке смежности.
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#define MAX 2010
#define INF 0x3F3F3F3F
using namespace
std;
int i, j, v, d, to, cost, n, m, s, f, b,
e, w;
int used[MAX], dist[MAX], parent[MAX];
vector<vector<pair<int, int> >
> g;
priority_queue<pair<int,int>,
vector<pair<int,int>
>,
greater<pair<int,int> > >
pq; //(distance,node)
void Relax(int
v, int to, int
cost)
{
if (dist[to]
> dist[v] + cost)
{
dist[to] = dist[v] + cost;
pq.push(make_pair(dist[to],to));
parent[to] = v;
}
}
void path(int
v)
{
if (v == -1) return;
path(parent[v]);
if (parent[v]
!= -1) printf(" ");
printf("%d",v);
}
int main(void)
{
scanf("%d
%d",&n,&m);
scanf("%d
%d",&s,&f);
g.resize(n+1);
for(i = 0; i
< m; i++)
{
scanf("%d
%d %d",&b,&e,&w);
g[b].push_back(make_pair(e,w));
g[e].push_back(make_pair(b,w));
}
memset(dist,0x3F,sizeof(dist));
dist[s] = 0;
memset(parent,-1,sizeof(parent));
memset(used,0,sizeof(used));
pq.push(make_pair(0,s));
while(!pq.empty())
{
v = pq.top().second; d = pq.top().first;
pq.pop();
if (d >
dist[v]) continue;
for(j = 0; j < g[v].size(); j++)
{
to = g[v][j].first;
cost = g[v][j].second;
if
(!used[to]) Relax(v,to,cost);
}
used[v] = 1;
}
if (dist[f]
== INF)
printf("-1\n");
else
{
printf("%d\n",dist[f]);
path(f); printf("\n");
}
return 0;
}
Реализация
алгоритма – очередь
с приоритетами, список смежности, собственная структура пары
Реализуем алгоритм Дейкстры при помощи очереди с приоритетами на списках смежности используя
собственную структуру пары (вершина, расстояние).
#include <cstdio>
#include <cstring>
#include <vector>
#include <queue>
#define MAX 2010
#define INF 0x3F3F3F3F
using namespace
std;
int i, j, v, d, to, cost, n, m, s, f, b,
e, w;
int used[MAX], dist[MAX], parent[MAX];
struct edge
{
int node,
dist;
edge(int
node, int dist) : node(node), dist(dist) {}
};
bool operator<
(edge a, edge b)
{
return a.dist
> b.dist;
}
vector<vector<edge>
> g;
priority_queue<edge>
pq;
void Relax(int
v, int to, int
cost)
{
if (dist[to]
> dist[v] + cost)
{
dist[to] = dist[v] + cost;
pq.push(edge(to,dist[to]));
parent[to] = v;
}
}
void path(int
v)
{
if (v == -1) return;
path(parent[v]);
if (parent[v]
!= -1) printf(" ");
printf("%d",v);
}
int main(void)
{
scanf("%d
%d",&n,&m);
scanf("%d
%d",&s,&f);
g.resize(n+1);
for(i = 0; i
< m; i++)
{
scanf("%d
%d %d",&b,&e,&w);
g[b].push_back(edge(e,w));
g[e].push_back(edge(b,w));
}
memset(dist,0x3F,sizeof(dist));
dist[s] = 0;
memset(parent,-1,sizeof(parent));
memset(used,0,sizeof(used));
pq.push(edge(s,0));
while(!pq.empty())
{
edge e = pq.top(); pq.pop();
v = e.node;
if (e.dist
> dist[v]) continue;
for(j = 0;
j < g[v].size(); j++)
{
to = g[v][j].node;
cost = g[v][j].dist;
if
(!used[to]) Relax(v,to,cost);
}
used[v] = 1;
}
if (dist[f]
== INF)
printf("-1\n");
else
{
printf("%d\n",dist[f]);
path(f); printf("\n");
}
return 0;
}
Реализация
алгоритма – матрица смежности
Реализуем алгоритм Дейкстры на матрице смежности.
#include <cstdio>
#include <cstring>
#include <vector>
#define MAX 2001
#define INF 0x3F3F3F3F
using namespace std;
int i, j, mn, n, m, s, f;
int b, e, len, v;
int g[MAX][MAX],
used[MAX], dist[MAX], parent[MAX];
void PrintPath(int v)
{
vector<int>
res;
while (v !=
-1)
{
res.push_back(v);
v = parent[v];
}
for (int i =
res.size() - 1; i >= 0; i--)
printf("%d
", res[i]);
printf("\n");
}
void Relax(int i, int j)
{
if (dist[i] +
g[i][j] < dist[j])
{
dist[j] =
dist[i] + g[i][j];
parent[j] = i;
}
}
int main(void)
{
scanf("%d
%d", &n, &m);
scanf("%d
%d", &s, &f);
memset(g, 0x3F, sizeof(g));
memset(used, 0, sizeof(used));
for (i = 1; i <=
m; i++)
{
scanf("%d
%d %d", &b, &e, &len);
g[b][e] = g[e][b] = len;
}
memset(dist, 0x3F, sizeof(dist));
dist[s] = 0;
memset(parent, -1, sizeof(parent));
for (i = 1; i <
n; i++)
{
mn = INF; v =
-1;
for (j =
1; j <= n; j++)
if
(!used[j] && dist[j] < mn) { mn = dist[j]; v = j; }
if (v
== -1) break;
for (j =
1; j <= n; j++)
if
(used[j] == 0 && g[v][j] != INF) Relax(v, j);
used[v] = 1;
}
if (dist[f] == INF)
printf("-1\n");
else
{
printf("%d\n",
dist[f]);
PrintPath(f);
}
return 0;
}
Java реализация
import java.util.*;
public class Main
{
static int g[][],
used[], dist[], parent[];
static final int INFINITY =
1000000000;
static void
PrintPath(int v)
{
if (v ==
-1) return;
PrintPath(parent[v]);
System.out.print(v + "
");
}
static void
Relax(int i, int j)
{
if (dist[i] + g[i][j]
< dist[j])
{
dist[j] = dist[i] + g[i][j];
parent[j] = i;
}
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
int m = con.nextInt();
int s = con.nextInt();
int f = con.nextInt();
used = new int[n+1];
Arrays.fill(used, 0);
g = new int[n+1][n+1];
for (int[] row: g)
Arrays.fill(row, INFINITY);
for(int i = 1;
i <= m; i++)
{
int b = con.nextInt();
int e = con.nextInt();
int distance = con.nextInt();
g[b][e] = g[e][b] = distance;
}
dist = new int[n+1];
Arrays.fill(dist, INFINITY);
dist[s] =
0;
parent = new int[n+1];
Arrays.fill(parent,
-1);
for(int i = 1;
i < n; i++)
{
int min = INFINITY, v =
-1;
for(int j = 1;
j <= n; j++)
if (used[j] ==
0 && dist[j]
< min) {min = dist[j]; v = j;}
if (v ==
-1) break;
for(int j = 1;
j <= n; j++)
if (used[j] ==
0 && g[v][j] != INFINITY) Relax(v, j);
used[v] =
1;
}
if (dist[f] == INFINITY)
System.out.println("-1");
else
{
System.out.println(dist[f]);
PrintPath(f);
System.out.println();
}
con.close();
}
}